Puzzle : Power game

Well,

I like the dramatic titles :-). Anyways, here goes the problem.

Problem : Given an integer n, determine whether for some integers a and b in poly-logarithmic time.

Solution : It is obvious that for certain n, there could be multiple a’s and b’s such that . We only need to find one such a and b or have to declare that there are no such integers. Needless to say, that we are ruling out b=1 :-).

Given any n, the number of bits required is log n. Now, let us fix b = 2. For this b,  a must be having bits. So we know the range of possible a’s that might satisfy . We do a binary search on this range in O(log n) time. If we do not find a suitable a, we fix b=3 and repeat. There can be only logarithmic many such b’s. Multiplication and calculating powers of a number, both can be done in polylog time. Hence, we can determine that the given number n is of the form for some n or not.

Cool, isn’t it?

–Saurabh Joshi

Puzzle : Find a duplicate

Well,

Needless to say that the puzzle was given by Ramprasad. After thinking for a while, I could figure out the solution using an old trick from one of the typical technical interview questions.

Problem : Given n element in an array ( say 0 to n-1 ). The elements comes from the set {1,..,n-1}. Clearly, due to pigeion hole principle, there will be a duplicate element. There can be more than one element which are occurring twice or more. In O(n) time, find out one duplicate element. The additional space you can use should not exceed O(log n).

 

Solution : At first, I thought that one can just have a bit array, storing whether we have seen an element or not. But for elements coming from 1,…,n-1 the number of bits required is O(n). Even if we consider a number representation to take O(log n), it will still require O(n/ log n) numbers to be stored. So clearly, that can not lead to a solution.

 

What works is as follows. Let us say you are given a singly linked list. You need to detect if the linked list has a cycle or not. You can only store constant many elements.

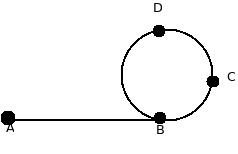What you can do is have two poiters, p1 and p2. At each  step, you increment p1 by 1 ( by increment we mean that go to the next element in the linked list ), and you increment p2 by 2. If p1 and p2 ever becomes same, that means that the linked list has a cycle, otherwise, p2 will hit the end of the linked list.

It is worth noting that in this scenario, p1 and p2 will meet before p1 can finish traversing the entire cycle. Also, for any two relatively prime numbers ( n1, n2), if you increment p1 by n1 and p2 by n2, they will still meet irrespective of the length of the cycle.

 

This seemed like a little diversion from our original problem, but we are going to use this :-). What we will do is, we will look inside the element at index 0. Let us say this element is e1. Now we will look in the array A, A[e1] and then A[A[e1]] and so on. We can think of this mechanism forming a singly linked list. Because the element ranges from 1,….n-1, and the total elements in the array being n ( from index 0 to n-1 ) there has to be a cycle in this list. And as shown in the figure, the starting point of the cycle B, is the element which is repeated twice.  That is because, B will have two distinct predecessor e1 and e2 such that A[e1]=A[e2] = B.

 

So what you do is the following. As mentioned earlier, have two pointers p1 and p2. p1 will move by 1 and p2 will move by 2. Say they meet at point C. Let us say that distance AB=p, BC= q and CDB=r. How much p1 must have traversed? It will be p + q where as p2 has traversed p+q+r+q = 2(p+q) ( double than p1).
So, p = r.

So once we reach C. We will move p1 to A ( that is start from index 0 again ) and keep p2 at C. Remember that AB=p=r=CDB. Now, we will move p1 and p2 both by 1. They will meet at B and that is our duplicate element :-).

Instead of moving p1 by 1 and p2 by 2 to find out the point C, what if we move then by (n1,n2) where n1 and n2 are relatively prime? Would it work? 🙂

 

–Saurabh Joshi