Increasing or decreasing subsequence

Well,

I found this problem here. Solution to the second puzzle given in that post is already posted in Kissa Kursi Ka. I tried a couple of approaches to solve the first one but could not succeed. Finally, Deepanjan came up with a very elegant solution, so the entire credit goes to him for providing the solution to the first problem.

Just now I saw a message from Saket that this problem is known as Erdős–Szekeres theorem. No wonder that Erdös was part of this fascinating problem.

For those who are wondering what I am talking about, I am copying the problem in question over here.

Problem : Given a sequence of r*s+1 distinct integers (r>=1, s>=1) prove that there exists either an increasing subsequence of length r+1 or a decreasing subsequence of length s+1 ( taken from viked’s blog )

Solution : The first observation is that r and s are interchangeable. Nevertheless, we will start proving that either we have a decreasing subsequence of length s+1 or an increasing subsequence of length r+1.

Let the sequence of distinct integers be where . We will start from . Now, select the next number which is less than . This way we can form a subsequence

. If we are done. If not, we will remove this subsequence from the original one. Also, note that for every element in the remaining sequence there exist an element such that . Repeat the same procedure again on the remaining sequence, we will have

and so on. If at any time we are done. If not, we can have at least r+1 different subsequences. For an element there exist an element . This way, we have an increasing subsequence

This proof by Deepanjan is so elegant that I would indeed call it a beautiful proof.

–Saurabh Joshi

Who can name the bigger number?

Well, I read a very interesting article long back. Just adding a link over here. It is a very interesting read.

http://www.scottaaronson.com/writings/bignumbers.html

Puzzle : Nuts and Bolts

Well,
This is a quite easy puzzle. It was asked to my friend Sanjeet Khaitan during one of the technical interviews in some company.

Problem : You are given a set of nuts and bolts of different sizes. Each nut has a corresponding unique bolt for it. We need to find out for each nut its corresponding bolt. The condition is that a nut can only be compared with a bolt and vice versa. So you can not compare two nuts and two bolts for their sizes directly. How would you do it?

Solution : Actually, this nut and bolt stuff is just an added complication. If we look at it, it is nothing but a quick sort algorithm. We can choose a nut as a pivot and using which we can partition bolts. Also during this process, we would have been able to find out its corresponding bolt. Using this bolt, we will partition nuts. Now recurse on left and right partition exactly the same way we do it for quick sort.

–Saurabh Joshi

Puzzle : Kissa Kursi Ka ( A matter of a seat )

Well,

I have read this puzzle a couple of times but never did I put my mind to it. Once deepanjan and I sat together to solve it. We both came up with two different solution, both correct. My laziness made me procrastinate posting the solution here. Anyways, now that I am on it, let me directly go to the puzzle.

Problem : There is an airplane and 100 passengers are given boarding pass for the same. The first passenger lost his boarding pass and he did not remember the seat number assigned to him. So, when this first passenger boards the plane he chooses one seat uniformly randomly. Rest of the passengers, board the plane in the sequence of 2 to 100. If a passenger finds his seat vacant, he will sit there, if not, he chooses a vacant seat uniformly randomly. The question is, what is the probability that the last person ( 100th in this case ) will find his seat vacant when he boards the plane?
Number 100 has nothing to do with the puzzle and we can as well state that there are passengers.

Solution 1 : Well, I have come up with this solution. I started initially with 2,3,4,5 passengers and found the probability manually. So I conjectured that the probability is 1/2 in all the cases. Now, the task remains is to prove that it is indeed the case for any . I remembered my favorite professor sundar vishwanathan and a very powerful mathematical tool that he taught us to use in a very elegant way. And mathematical induction indeed helped me proving my conjecture.

Base case : n=2.

Clearly, the first person sits in the 2nd person’s seat with probability 1/2. So the last person ( 2nd person in this case ) finds his seat vacant with the probability 1/2.

Hypothesis : For any 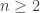probability that the last person finds his seat vacant is 1/2.

Induction Step : Let there be n+1 passengers.

Let 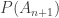= probability that n+1 th person finds his seat vacant when there are total n+1 seats.

Let 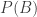= probability that at least one person of the first n persons ( say k th person ) found his seat vacant hence he sat in his own seat.

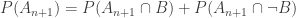
It is clear that 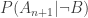is 1/2. Because, when none of the first n person find their seat vacant, it must be the case that 1st person seats in 2nd seat, 2nd person seats in 3rd seat and so on. Because they arrive in sequence, if 1st person seats in 3rd seat, then 2nd person would find his seat vacant. Or if 2nd person seats in 1st seat, then 3rd person would find his seat vacant. So after n-1 person take their seats, only two seat ( 1st and n+1 th ) remains vacant. Now the n th person chooses the 1st seat with the probability 1/2 which is precisely the probability that the last person ( n+1 th ) person would find his seat vacant given that none of the first n could find their seat vacant.

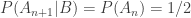. The reason is that, if at least one person of the first n persons could find his seat, then we can view it as if k-th seat was already taken when the first person boarded the plane. We can view it like that because we are given that event B has happened and now we have to find the probability of all other events that are occurring. So original problem of n+1 person and n+1 seats reduces to n person and n seats for which we can use induction hypothesis.

Let .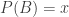

So, .
So irrespective of how many persons and seats are there, the probability remains constant.

Solution 2 : Deepanjan came up with this solution. Given n person, his solution looks like this.

Let 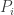denote the fact that i-th person does not find his seat vacant.

because the first person chooses the 2nd seat with probability 1/n.

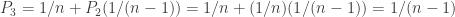because, either first person choose the 3rd seat with the probability 1/2 or the 2nd person find his seat taken and chooses 3rd seat with probability 1/(n-1).

Similarly,

In general, it should be easy to see that for . Hence, for the last person when i=n we have 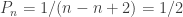. The probability that n-th person finds his seat vacant would be 1 – (1/2) = 1/2.

–Saurabh Joshi

Puzzle : Form a triangle

Well,

This is a very easy puzzle for those who know a little bit of maths. This was asked at IIT Kanpur in PG admission test.

Problem : Given a stick of 1 meter, two points are chosen uniformly randomly to cut the stick. What is the probability that 3 pieces so generated would form a triangle?

Solution : The way I solved it is this. Clearly, to form a triangle it must satisfy triangle inequalities, that is if and are three sides then , and . Or if we look at it other way, none of the piece should be great or equal to 0.5 meter. So we need to answer, what is the probability that none of the piece measure greater or equal to 0.5?

Let (because of symmetry) be the first point from left side where the stick is cut. It is clear that to ensure that none of the piece measures the second cut-point must be such that . So for the second cut point feasible region is of the length .

So,

Puzzle : Cross the bridge

Well,

This is yet another cross-the-bridge puzzle. This puzzle was posted on our group list by my friend Manoj Gupta. Without circling around, let me directly come to the point.

Problem :

M – Mother

F – Father

s1, s2 – sons

d1,d2 – daughters

P – Policeman

T – Thief

They are all standing at one side of the bridge. There is only one car with the capacity of two people. Only M, F or P can drive. The catch is that the father is hostile towards the daughters, and mother is hostile towards the sons. So if the mother is not there to protect the daughter, the father would kill them even he gets this chance for a second.  Similarly, if father is not around to protect the son, mother would kill the sons. And when policeman is on the other side of the bridge, the thief would kill everybody on the same side of the bridge as his. How can they all cross the bridge safely ?

Solution : Following is the state sequence that would give the trace how we can move everybody safely to the other side.

MFs1s2d1d2PT = _ ( Initial configuration )
MFs1s2d1d2 = PT ( Police drives thief to the other side )
MFs1s2d1d2P = T ( P comes back )
MFs1s2d1 = PTd2 ( P drives d2 to other side )
MFs1s2d1PT=d2  ( P comes back with T )
Fs1s2PT=Md1d2 ( M drives d1 to the other side )
MFs1s2PT=d1d2 ( M comes back )
s1s2PT=MFd1d2 ( M drives F to the other side )
Fs1s2PT=Md1d2 ( F comes back )
Fs1s2=Md1d2PT ( P drives T to the other side )
MFs1s2=d1d2PT ( M comes back )
s1s2=MFd1d2PT ( M drives F to the other side )
Fs1s2=Md1d2PT ( F comes back )
s2=Fs1Md1d2PT ( F drives s1 to the other side )
PTs2=Fs1Md1d2 ( P comes back with T )
T=Fs1s2Md1d2P ( P drives s1 to the other side )
PT=Fs1s2Md1d2 ( P comes back )
_=Fs1s2Md1d2 ( P drives T to the other side )

I have seen earlier puzzle when you have to cross the river with Tiger, Goat and Grass
but I guess this one has more constraint.

--Saurabh Joshi

Cake Cutting Algorithms – 6 : Fair Convex Partitioning

Well,

This post is a digression in the series of posts which discussed about cake cutting algorithms, in a sense that definition of “fair” changes in this article and it introduces a new concept of convex partitioning. I acknowledge my dear friend rik for bringing this problem to my notice.

Problem : A cake is to be divided amongst people. The condition is that each one should get a single piece, so all these pieces have to be of the same size. ( By “same size” we mean that volume of the cake has to be same. In this case, given any piece, everybody would evaluate it to posses the same value, which was not the case for earlier articles. ) Entire cake is homogeneous so if we look the cake from the top, we need to divide the cake into exactly n pieces such that area of the top view of every piece has the same area. Furthermore, the frosting would be poured onto the pieces after they have been cut, so all pieces should have equal perimeter. Looking from the top, cake is a convex set.

So, the cake ( a 2-d convex set ) has to be divided in pieces of equal area and equal perimeter.

Solution : Well, those who are looking curiously for a solution, I am sorry to say that this problem is an open problem in general. That is, it is yet unknown whether for any given and any given convex set such a partitioning even exist and if so, how to achieve such a partitioning. For more details one can visit this web page.

However, for the proof that a partitioning exist is very easy. The proof is based on intermediate value theorem which states that for a continuous function if then there exist a point such that .

Claim 1 : Given any direction, there exist a line which bisect the convex set into two parts such that they have equal area.

Proof : For any given direction, let’s have a line such that the entire convex set is below the line. Let us define a function such that fraction of area of the convex set above the line, where denotes the intersection point between the line and . Now, slowly move the line downwards so that it intersects with the convex set. So, initially and at the end . So intermediate value theorem tells us that there exist a line when . When, the direction is parallel to we can use x-intercepts.

Claim 2 : There exist a line which divides the convex set into two pieces so that the area and the perimeter of those pieces are equal.

Proof : From Claim 1, we know that for any given direction we can have a line which bisect the set area wise. Let us define a function such that (perimeter of the piece above the line – perimeter of the piece below the line), where denotes the angle the line makes with . Let us say we start with and end with . If then because line has rotated 180 degree and the pieces switch their places. Again, due to intermediate value theorem we have that there exist a such that . At this point, two pieces will have equal area as well as equal perimeter.

For this proof, I took inspiration from one of my post about necklace theorem.

–Saurabh Joshi

Puzzle : Two piles of equal cards facing up

Well,

I came across this extremely simple puzzle which looked a bit difficult initially.

Problem : You are in a dark room ( or completely blind folded ) and you are given a standard 52 card deck out of which 13 cards are facing up and rest all are facing downwards.  You have to divide the deck into two piles so that number of cards facing up in both the piles are equal. You are allowed to flip any card as many times as you want, however, you can’t tell whether a card is facing up or facing down by touching it.

Solution : Take any 13 cards and flip them all. Rest 39 cards will make another pile. These two piles will have the same number of cards facing up. Why? Well, say out of those 13 selected cards are facing up.  Which means that in the pile with 39 cards there will be cards facing up. When you flip all 13 cards, number of cards facing up now becomes which is equal to what the other pile have.

Puzzle : Guess a card

Well,

Without any preface, I am just coming to the point.

Problem : You have standard deck of 52 cards. You are allowed to choose 5 cards randomly. Now, you hand over four cards one after another to your partner. The problem is that your partner should be able to guess the fifth card remaining in your hand correctly. What strategy would you devise to communicate the fifth card to your partner? Please note that you can not use orientation of the card ( handing it over to your partner with 90 degree tilt ) or any facial expression or any gestures. The only things that you have to use for communication are 1) choosing which four cards to hand over 2) order in which you hand them over to your partner.

Solution :

I saw this puzzle at a couple of place and I was wondering wow, it must be tricky to use only 4 cards and locate a card out of 48 possibilities. But as I put my mind to it, this puzzle seemed extremely simple to me. Here is the strategy that you and your partner can follow.

Note that, because you have chosen 5 cards, there must be at least two cards of the same suite because of pigeon hole principle. This way definitely you can communicate in which suite the fifth card belongs. Now let us have an ordering of the suites. Spades < Hearts < Diamond < Clubs. So, the first card that you would hand over to your partner would be of the same suite as the fifth card.

Now, we have narrowed down the possibilities to 12 cards ( as 1 card of the same suite has already been handed over to the partner ). It seems that now we have 3 cards left and 12 possibilities. How can we communicate a number upto 12 with only 3 cards? It turns out that we don’t need an ability to communicate a number up to 12. There is a circular ordering in the suite. so Ace < 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < Jack < Queen < King < Ace. By this scheme, the maximum distance between any two cards is 6. Now, we have 3 cards to communicate a number up to 6. well, 3! = 6. We can use permutation of remaining three cards to communicate this number.

But for , permutation we need a total ordering. We have already ordered the suites. And within the suite we will follow ordering of Ace < 2 .. < 10 < Jack < Queen < King ( We can’t use circular notion over here for obvious reason ). For example “King of Spades” is smaller than “2 of Hearts”. Remaining three cards now can be viewed in ascending order.

For example “King of Spade”(1) < “5 of Diamond” (2)< “7 of Diamond”(3). We can assign them numbers as indicated in the bracket. Now, we can assign number to the permutations :

123 = 1

132 = 2

213 = 3

231 = 4

312 = 5

321 = 6

Order in which you hand over the remaining 3 cards would indicate the minimum distance between the first card handed over and the card to be guessed ( the fifth card ). But how do we communicate the direction of the distance ? Counting up? or Counting down? Well, we don’t have to. The trick lies in picking up the card out of 2 cards of the same suite. For example “4 of Spade ” and “Queen of Spade”. You can tell your partner to always count upwards. Which card to hand over as the first card? If we hand over “4 of Spade” then distance in up direction is 7 ( as Queen = 11 ). So we would hand over the “Queen of Spade”. Queen < King < Ace < 1 < 2 < 3 < 4 = 6 hops ( or distance ).

To summarize, the first card should be chosen such that it has the same suite as the 5th card as well as distance in up direction should be at most 6.

Pretty neat, isn’t it?

–Saurabh Joshi

Cake Cutting Algorithms – 5 : Envy Free Division

Hi All,

It has been ages since I have posted anything on cake-cutting. But now, I am back and as I promised in my previous post on the same topic I am posting about envy free division. We have already seen in the last post on cake-cutting what envy-free division means.

What is the motivation behind envy-free division? Well, as saint kabir said :

दुनिया अपने दुःख से उतनी दुःखी नहिं है, जीतनी दूसरों के सुख से है |

— संत कबीर

Let us recall our old friends Pinku and Chinku. How do we divide a cake between them so that the division is envy free? It is easy to see that cut-and-choose algorithm would render an envy free division of the cake. The cutter would be envy free because from cutter’s point of view both the pieces are same. The chooser also remains envy free because he gets to choose the largest piece.

What if Rinku joins the party? Now, things get a bit complicated.

We will let Pinku cut the cake in 3 equal pieces named . If largest piece from Rinku and Chinku’s perspective are different than we are in a good shape. Because we can give Rinku and Chinku whichever piece they desire and the remaining piece to Pinku. Pinku is still envy free because from his point of view all three pieces were equal. This is an example where disagreement between people makes things easy.

What if Rinku and Chinku both desire to get the same piece. We will let Rinku arrange three pieces in an order so that . Now, if we will let Rinku cut such that from her perspective. Let the trimmed piece be called .

Let Chinku choose any one piece between . Rinku can choose whichever piece is left, that is either or . If however, should Chinku choose we insist that Rinku take . Chinku is envy free because he got his piece of choice. Rinku is envy free because she got or which she believed to be of equal size but larger than . Pinku is envy free because he gets either or which he believed to be of equal size but larger than .

What about the left over ? We know that even if entire is given to the person who got Pinku would be envy free to that person as from his point of view . Without loss of generality let us assume that Chinku got . Then we will let Rinku cut into 3 equal pieces. Out of these three, let Chinku choose first, it is obvious that other two will remain envy free of Chinku. Let Pinku choose second and Rinku will get the remaining piece.

So we have achieved an envy free division of cake amongst 3 persons. Things get more complicated as more number of persons participate in the division.