Let there be light!!!

It has been a long time since I have posted anything on my blog. Well, I guess I am just out of focus now a days. Anyways, today’s post is not about a puzzle but it is rather about a couple of open problems. I apologize for not giving any reference for these problems.

Problem 1 :

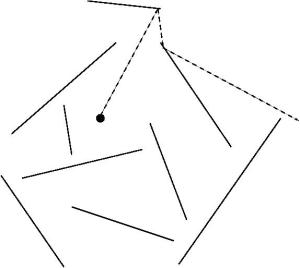
There are finite number of  non-intersecting line segments in a 2D plane. Each of these line segments act as a mirror from both sides. That is, any ray incident at an angle is reflected back at an angle where . It is conjectured that for any point in the 2D plane. If a light source is put at then there will be at least one light ray which will escape to infinity ( or in other words, the path of the light ray can not be bounded by a closed curve on the 2D plane ). No other physical phenomena like refraction, deflection etc can be used for the argument.

This innocuous looking problem is notoriously hard to prove or disprove.

Problem 2 : Let there by any polygon in a 2D plane. It has been conjectured that if a light source is put at any point in the polygon, it will illuminate the entire polygon ( for each point in the polygon, there exist a ray from light source which reaches at point observing only the law of reflection as described in the Problem 1 ).

This is again an open problem and so far it is invincible. Any takers???

–Saurabh Joshi