Cake Cutting Algorithms – 7 : Divide and Conquer

Well,

It has been long since I have written anything about cake-cutting. Anyways, in this post I am going to describe the best known deterministic algorithm for cake-cutting.

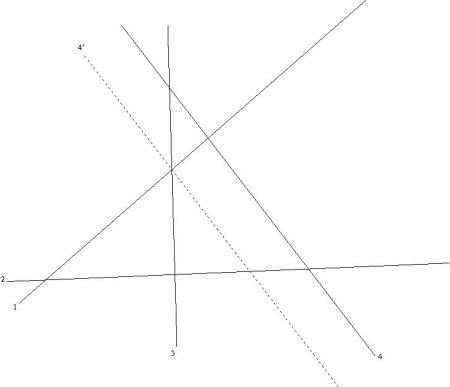
Let’s say we want to divide the cake between 4 people. We can let p1,p2,p3 mark a line which will divide the cake in two equal halves according to their own perceptions (captured by evaluation function ).

Say for example, p1,p2 and p3 marks line as shown in the figure. Because odd number of persons have cut the cake we can have a middle line. We will cut the cake at this line. Ask p4, whether the piece on the left or right is at least half according to his perception. If p4 selects the left half, then play cut and choose between p4 and p1 for the left piece and for p3 and p2 for the right piece. It is easy to work out the solution in case p4 selects the right piece.

What if there are odd number of people? Say 5. In this case, we will ask p1 to p4 to mark the lines which will cut the cake in the ration 2:3 from the left. Ask, p5 if he thinks whether the left piece is worth at least 40% or the right piece is worth 60%. As argued above, we can divide group into bunch of 2 and 3 and recurse.

So in general, if n is even, ask first n-1 people to cut the cake in the ratio of 1:1. If n is odd, ask first n-1 people to cut the cake in the ratio (n-1)/2 : (n+1)/2. And then ask which piece the n-th person thinks is worth at least its declared value.

It is easy to see that this algorithm works in time . This is the best known deterministic algorithm for simple fair division.

It has been conjectured that the simple fair division can not be achieved in with a deterministic discrete ( unlike moving-knife algorithm ) algorithm.  Many believe that the lower bound for simple fair division, where queries to evaluation function is not free, is . However, it is an open question that remains to be answered.

— Saurabh Joshi

Particle Collisions

Hi All,

It has been a long break on this blog. I was heavily busyb with some work. Anyways, lets get down to the business.

We are hearing buzz about CERN and the mightiest particle accelerator it created on which the “big bang” experiment has been started. And it so happened that I came across this nice puzzle, thanks to Sagarmoy.

Problem : 4 particles are travelling with mutually different uniform velocity ( uniform velocity implies that the speed is constant as well as the direction of motion does not change ).

We will say collision occurred between two particle when two particles are at the same place at the same time. Our particles being of a special kind, do not change their velocity even after the collision. You can imagine that particle can pass through the other.

The velocity vectors of these 4 particles are mutually non-parallel. Also, it is given that only 2 particles will participate in any collision ( no three line co-incide at the same point ).

Given these facts, we know that minimum 0 (no two lines are on the same plane) and maximum 6 collisions () can occur. If it is known that 5 collisions have occurred, can you prove that 6th collision will always occur?

Solution : Well, there are two solutions. One by Sagarmoy and one by Deepanjan. I will describe Deepanjan’s solution first.

1) As shown in the figure, lines 1,2,3,4 indicate the direction of particle motions. Let’s say we want to know that when 5 collisions have occurred ( all but (3,4) ) then collision between (3,4) will always occur.

Let’s have a line 4′ parallel to line 4. We know that collision (1,4) and (1,3) has occurred. As line 4′ is parallel to line 4, it is easy to see that collision (1,4′) would also occur because the ration of distance needed to be travelled within a given timeframe for both the particles does not change. We also know that (1,3) collision has occurred. So obviously (3,4′) collision would also occur. Again, as 4′ is parallel to 4, (3,4) collision would definitely occur.

Similar proof can be given for any different orientation of lines.

2) This solution is by Sagarmoy and it quite elegant, I must say. Consider the path of particle in space-time ( 4-dimensions , 3 physical + 1 time). As the particles travel with uniform velocity, their path corresponds to lines in space-time. Again, let us say, we want to prove that collision (3,4) will occur if all other 5 collisions has occurred.

We know that collisions (1,2)(1,3)(2,3) has occurred. So, line 3 must lie on the plane defined by line 1 and line 2. Similarly we know that (1,2)(1,4)(2,4) has occurred, so line 4 also must lie on the plane defined by line 1 and 2. So, line 3 and 4 are on the same plane and are not parallel. It must happen that lines intersect. But intersection of lines in space-time means that particles are at the same place at the same time, so collision (3,4) must occur.

— Saurabh Joshi